Output Transformer Impedance

Determining Output Transformer Impedance

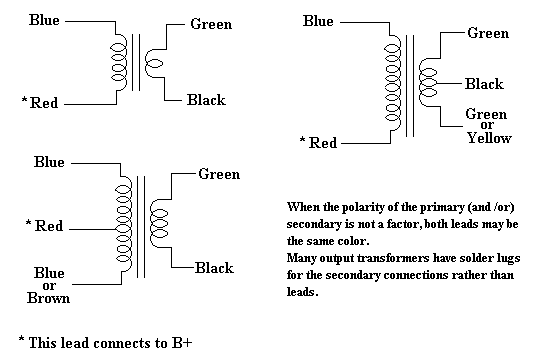
When replacing the audio output transformer on a radio, the replacement should match the impedance of the original as close as possible. If the wrong transformer is used, the results can be low output and loss of tone quality. Universal output transformers are available which have multi-tapped primary and secondary windings to match a wide impedance range.

It is not uncommon for the vintage radio collector to have various output transformers laying about that have been pulled from parts sets, or have been obtained at swap meets. Often times, the primary and secondary impedance information is not available for these units, and it would be nice to have that information to be able to use these in a set that needs a new output transformer.

The average beam power output tube, such as the 6V6 requires a load of around 5,000 ohms, and the average speaker voice coil can vary from as low as 1 ohm to 8 ohms or more. So, how do we determine which of our output transformers will match that impedance range? With some simple test equipment and ohms law, we can calculate the impedance of an output transformer, but first lets look at the function of an output transformer and how it works.

Function And How It Works

A tube is a high-voltage/low-current (high-impedance) device, while a speaker is a low-voltage/high-current (low-impedance) device. The function of the audio output transformer is to transform the high impedance of the output tube to match the much lower impedance of the speaker. This is necessary to get an efficient transfer of the audio signal to the speaker. The output transformer as an impedance matching device, works on the principal of reflected load. To help explain this, refer to figure 1 below.

To keep the math simple, lets assume an output tube is supplying a 100 volt ac signal to the primary of an output transformer with a 10:1 winding ratio, and the secondary is feeding a 10 ohm voice coil (see figure 1A below). With 100 volts across the primary, there will be 10 volts across the voice coil connected to the secondary. Using ohms law, there will be 1 amp of current flowing in the voice coil.

   I = E/R
   I = 10/10 = 1 ampere

For further simplification we will assume 100% efficiency in the transformer. Since we have a 10:1 ratio, the current flowing in the primary will be .1 ampere ( 1 amp in secondary divided by 10). With 100 volts across the primary, ohms law tells us that the primary looks like a 1,000 ohms impedance load to the tube.

   Z = E/I
   Z = 100/.1 = 1,000 ohms

Now if we decrease the impedance of the load, what happens to the impedance in the primary? If we place another 10 ohm voice coil in parallel with the original one, we now have a 5 ohm load (see figure 1B below). Using ohms law again we see that the current in the secondary is now 2 amperes.

   I = E/R
   I = 10/5 = 2 amperes

This means that the current in the primary also doubles to .2 amperes. Again using ohms law, the impedance of the primary is now 500 ohms.

   Z = E/I
   Z = 100/.2 = 500 ohms

This is called the reflected load. A 10 ohm load reflects back a 1,000 ohm impedance, while a 5 ohm load reflects back a 500 ohm impedance. The reflected impedance is a function of the turns ratio of the transformer. Notice that the ratio of the primary impedance to the secondary impedance is the square of the turns ratio, or 100:1. In other words, a 10:1 turns ratio will give an impedance ratio of 100:1.

**Figure 1**

Checking An Unknown Output Transformer

We can now use this knowledge to determine the impedance of any unknown output transformer. All we need to do is determine the turns ratio of the transformer, and with that information we can calculate what impedance will be reflected back to the primary with a given load on the secondary. The test equipment to do this is quite simple; an ac voltmeter and a variable source of 60 Hz ac is all we need.

To determine the turns ratio we apply an ac voltage to the primary, and measure the voltage in the secondary. The voltage on the secondary will be stepped down by a proportional amount determined by the turns ratio of the transformer. Figure 2 below shows the schematic diagram of the test set-up. A variable auto-transformer (sometimes referred to by the brand name Variac) is used to apply the variable ac to the primary (see note below). An ac voltmeter is connected to the secondary to measure the output voltage. To make the calculation of the turns ratio easy, the input voltage is increased until the voltage on the secondary reads 1 volt. With the secondary reading 1 volt, measure the input voltage to the primary. Since the voltage on the secondary is set to 1 volt, the voltage measured on the primary will be the turns ratio. For example, if the voltage on the primary measures 25 volts, the turns ratio is 25:1 as illustrated in figure 2 below.

Note: An auto-transformer does not provide isolation from the ac line. For safety reasons, the auto-transformer should be used in conjunction with a 1:1 isolation transformer.

**Figure 2**

Now, armed with the turns ratio, we can calculate the impedance ratio and the impedance that will be reflected to the primary with a given load in the secondary. Remember we said earlier that the impedance ratio is the square of the turns ratio. With our 25:1 turns ratio transformer in figure 2, the impedance ratio is the turns ratio squared or, 25 X 25 = 625:1. So if the transformer is working into an 8 ohm load, the impedance that will be reflected to the primary will be the impedance ratio (625) multiplied by the load impedance (8 ohms), equal 5,000 ohms. If the load in the secondary is changed to a 4 ohm load, the reflected impedance in the primary would be 625 X 4 = 2,500 ohms.

So it can be seen that the turns ratio of the transformer determines what impedance will be reflected to the primary by the load impedance of the secondary, and that an improper load on the secondary can have several effects:

if the load impedance is too low this will increase the current in the transformer windings. This also reduces the primary impedance that the output tube sees which increases tube current flow.
if the load impedance is too high, this reflects a higher than normal impedance in the primary for the output tube.
poor sound quality and lack of volume.

The impedance load seen by the tube and output transformer is not constant. The frequency of the audio signal will vary over a wide range. The inductance in the windings will have a different impedance at different frequencies. At a certain frequency an 8 ohm voice coil may have an impedance of 10 ohms or at low frequencies it my have an impedance of 4 ohms. This varying load impedance is reflected back to the primary, so the tube, and output transformer must work into a varying impedance range.

Chosing A Replacement Output Transformer

Now lets assume we have a set that has an output transformer with an open winding that must be replaced, and the output tube is a single 6F6. The schematic will sometimes give the dc resistance of the windings but that doesn't help us know what impedance the transformer should be. First we look at the chart below and see that a 6F6 should work into a load resistance of approximately 7,000 ohms. What about the speaker voice coil impedance? If we do not know the voice coil impedance we can get a fairly good estimate by measuring the dc resistance of the coil and multiply by 1.25. Lets say this one measures 6.5 ohms, multiplied by 1.25 = 8.125 so we could call this an 8 ohm voice coil.

With this information we can determine what the turns ratio should be. By dividing the secondary load of 8 ohms into the 7,000 ohms required by the 6F6, we get an impedance ratio of 875:1. If the impedance ratio is the square of the turns ratio, then the turns ratio is the square root of the impedance ratio. Taking the square root of 875 gives us a 29.6:1 ratio, so an output transformer with a turns ratio in this range should work.

By using the test procedure outlined above we can test our spare output transformers to see if we have one that will meet our approximate 30:1 turns ratio requirement.

Wattage Rating

Output transformers are rated in wattage. A good rule of thumb is that the replacement transformer should be about the same size as the original. If the replacement has the same size core or larger it should handle the wattage OK.

Chart Showing Approximate Plate Load Resistance
For Various Output Tubes
Primary Load Impedance	18,000	14,000	10,000	8,000	7,000	5,000	4,000	2,000
Single Ended Class A	1F4 1F5	1J5 1LB4 1T5 10 12A 12A7 38	6G6 19 41 49	1C5 1G5 1Q5 1S4 3Q5 3S4 6K6 6A4 7A5 7B5 12A6 14A5	2A5 6F6 12A 42 47	3B5 6AQ5 6L6 6V6 7C5 12A5 14C5 50 71A	6AC5 12A4 43 45 117L7	2A3 6Y6 7A5 25L6 35A5 35B5 35L6 48 50A5 50B5 50L6
Push Pull Plate to Plate		6K6 47	6AQ5 6F6 6L6 6V6 42	6V6 12A5 50 71A		2A3 45

Note: The load resistance will vary somewhat depending upon the voltages applied to the tube and the type of bias (fixed or self-bias). Consult a tube manual for actual load resistance under different voltages and bias.

**RMA Color Codes For Output Transformers**